Random Smoothing Regularization in Kernel Gradient Descent Learning

[JMLR 2024]

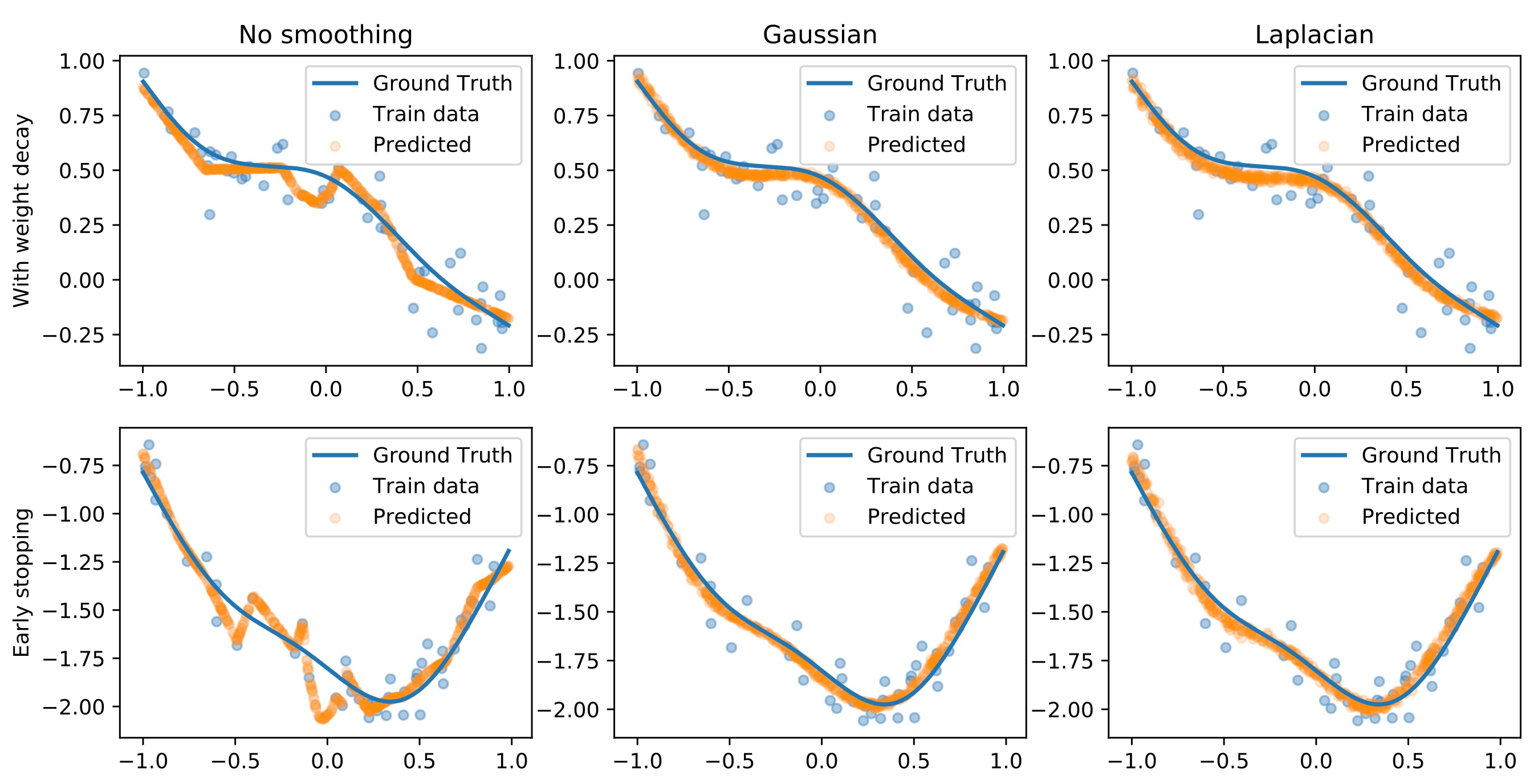
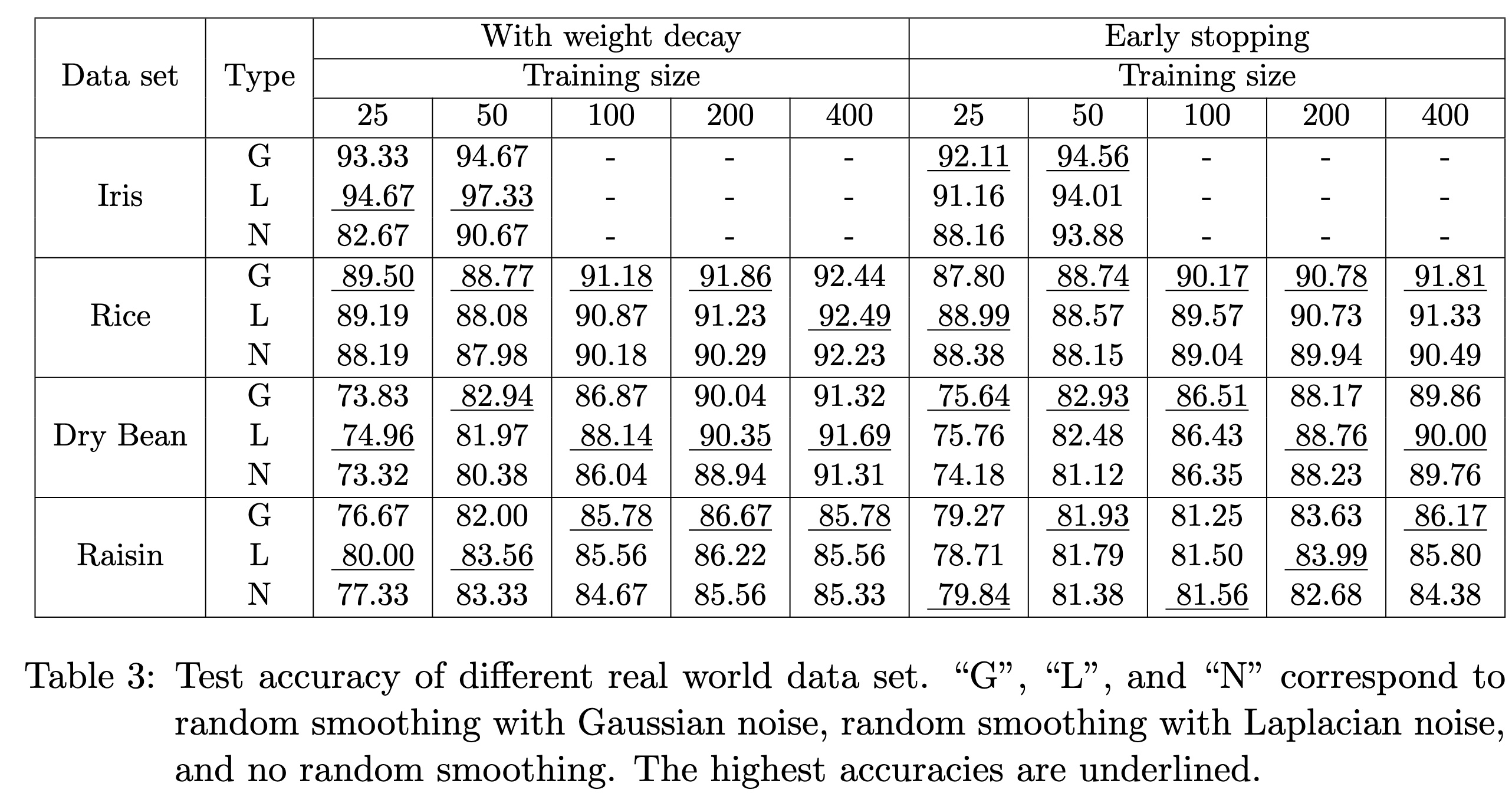
Random smoothing data augmentation is a unique form of regularization that can prevent overfitting by introducing noise to the input data, encouraging the model to learn more generalized features. Despite its success in various applications, there has been a lack of systematic study on the regularization ability of random smoothing. In this paper, we aim to bridge this gap by presenting a framework for random smoothing regularization that can adaptively and effectively learn a wide range of ground truth functions belonging to the classical Sobolev spaces.

Theoretical Results

(1) In case of Sobolev space of low intrinsic dimensionality $d\leq D$: When using Gaussian random smoothing, an upper bound of the convergence rate is achieved at $n^{-m_f/(2m_f+d)}(\log n)^{D+1}$, which recovers the existing results\textsuperscript{[2]} but we present a different approach that allows us to analyze polynomial smoothing; When using polynomial random smoothing with data size adaptive smoothing degree, a convergence rate of $n^{-m_f/(2m_f+d)}(\log n)^{2m_f+1}$ is achieved, which is again, hypothetically optimal up to a logarithmic factor.

(2) In case of mixed smooth Sobolev spaces, using polynomial random smoothing of degree $m_\varepsilon$, a fast convergence rate of $n^{-2m_f/(2m_f + 1)}(\log n)^{\frac{2m_f}{2m_f+1}\left(D-1+\frac{1}{2(m_0+m_\varepsilon)}\right)}$ is achieved, which is optimal up to a logarithmic factor.

Numerical Studies

Experiments on Real-world Dataset